Cost Minimization

  • A firm is a cost minimizer if it produces any given output level (y > 0) with the smallest possible total cost
  • Note that factor and input are synonyms in this chapter; they are interchangable
When the firm faces given input prices w=(w1,w2,...,wn)the total cost function will be written as c(w1,...,wn,y)\text{When the firm faces given input prices } w = (w_1, w_2, ..., w_n) \\ \text{the total cost function will be written as } c(w_1, ..., w_n, y)
  • Note that the total cost function does not include the amounts of inputs; this is because the total cost function is implied to use the optimal amount of inputs to minimize costs
    • In other words, the total cost function gives the firm’s smallest possible total cost for producing y units of output given input prices w = (w1, …, wn)

Cost Minimization Problem

  • Given two inputs and one output, we get the production function y = f(x1, x2)
  • Given the input prices w1, w2, the cost of an input bundle (x1, x2) is w1x1 + w2x2
Given w1,w2,y, the firm’s cost minimization problem is min{w1x1+w2x2} such that f(x1,x2)=y\text{Given } w_1, w_2, y \text{, the firm's cost minimization problem is } min\{w_1 x_1 + w_2 x_2\} \text{ such that } f(x_1, x_2) = y

The levels x1*(w1, w2, y) and x2*(w1, w2, y) in the least costly input bundle are the firm’s conditional demands for inputs 1 and 2.

The smallest possible total cost for producing y output units is therefore c(w1, w2, y) = w1x1*(w1, w2, y) + w2x2*(w1, w2, y)

Isocost Lines

  • An isocost curve contains all the input bundles that cost the same amount
  • The isocost curve is extremely similar to the budget constraint, even sharing similar equations
Given w1 and w2, the equation of an isocost line with a cost of c is w1x1+w2x2=cThis can also be written as x2=−w1w2x1+cw2\text{Given } w_1 \text{ and } w_2 \text{, the equation of an isocost line with a cost of c is } w_1 x_1 + w_2 x_2 = c \text{This can also be written as } x_2 = -\frac{w_1}{w_2} x_1 + \frac{c}{w_2}
  • The graph of isocost lines is therefore a series of parallel lines, with lower costs being closer to the origin

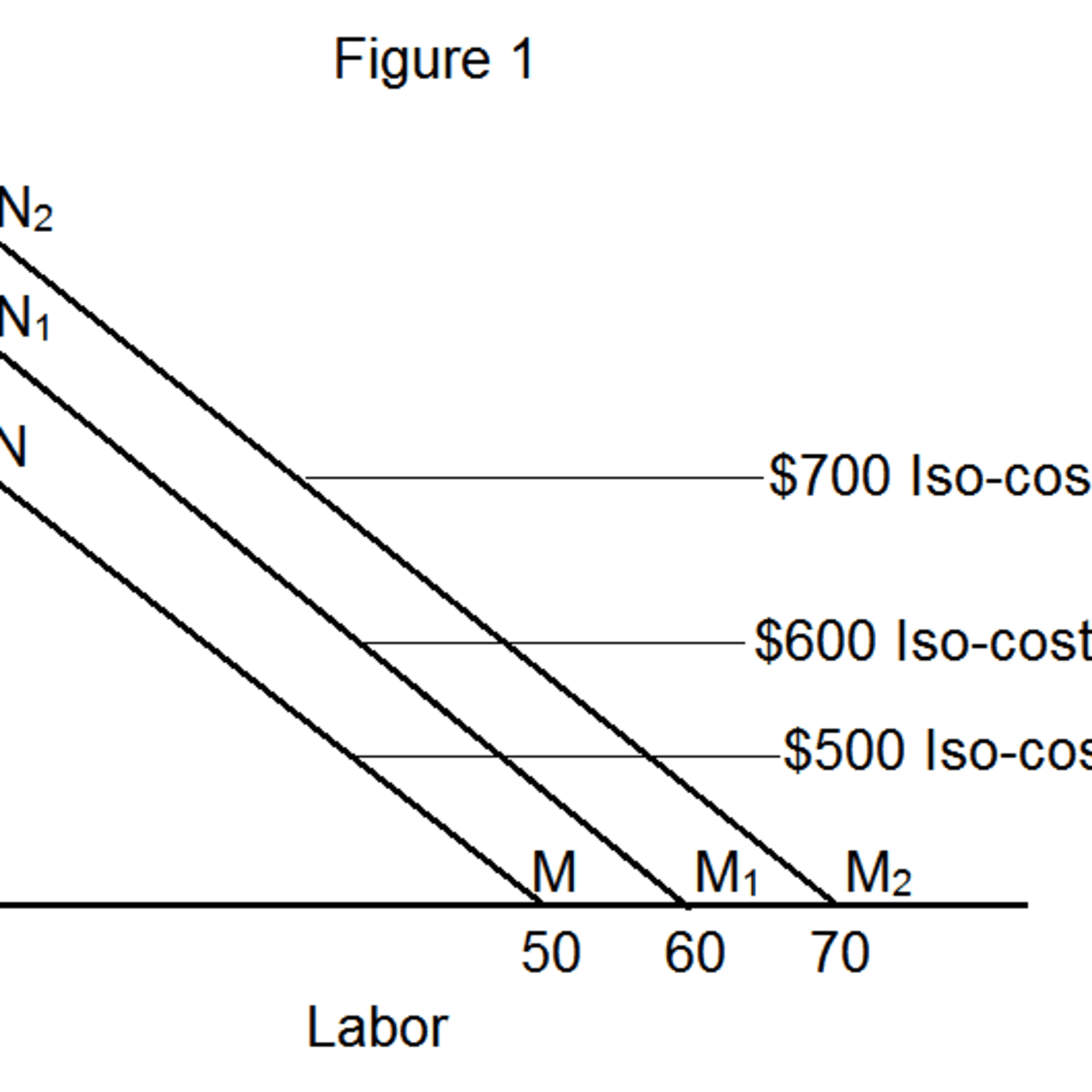
Isocost lines

  • To minimize costs, we must find the lowest possible isocost line that is tangent with the isoquant curve corresponding to a given output level

Isocost Isoquant Graph

  • To find the cost minizing bundle, set the slope (TRS) of the isoquant curve equal to the slope of the isocost curve
At an interior cost-minimizing input bundle:f(x1∗,x2∗)=y′Slope of isocost = slope of isoquant, or −w1w2=TRS=−MP1MP2 at (x1∗,x2∗)\text{At an interior cost-minimizing input bundle:} \\ f(x_1^*, x_2^*) = y' \text{Slope of isocost = slope of isoquant, or } -\frac{w_1}{w_2} = TRS = -\frac{MP_1}{MP_2} \text{ at } (x_1^*, x_2^*)

Cobb-Douglas Example

y=f(x1,x2)=x11/3x22/3 with input prices w1,w2Must satisfy two conditions: y=x11/3x22/3−w1w2=−MP1MP2=x2∗2x1∗From the second condition: x2∗=2w1w2x1∗y=(x1∗)1/3(2w1w2x1∗)2/3=x1∗(2w1w2)2/3x1∗=y(w22w1)2/3x2∗=2w1w2y(w22w1)2/3=(2w1w2)1/3yy = f(x_1, x_2) = x_1^{1/3} x_2^{2/3} \text{ with input prices } w_1, w_2 \\ \text{Must satisfy two conditions: } \\ y = x_1^{1/3} x_2^{2/3} \\ -\frac{w_1}{w_2} = -\frac{MP_1}{MP_2} = \frac{x_2^*}{2x_1^*} \\ \text{From the second condition: } x_2^* = \frac{2w_1}{w_2} x_1^* \\ y = (x_1^*)^{1/3} (\frac{2w_1}{w_2} x_1^*)^{2/3} = x_1^* (\frac{2w_1}{w_2})^{2/3} \\ x_1^* = y (\frac{w_2}{2w_1})^{2/3} x_2^* = \frac{2w_1}{w_2} y (\frac{w_2}{2w_1})^{2/3} = (\frac{2w_1}{w_2})^{1/3} y