Demand; Comparative Static Analysis of Choice

Demand Chapter

Own-Price Changes

$$\text{How does } x_1^* (p_1, p_2, y) \text{ change as } p_1 \text{ changes, holding } p_2 \text{ and } y \text{ constant?} \\ \text{Suppose } p_1 \text{ increases from } p'_1 \text{ to } p'_2 \text{ to } p'_3$$

The following graphic has two curves. The curve containing all the utility maximizing bundles as p₁ changes with p₂ and y constant is the p₁ price offer curve. The other graph plotting the x₁ coordinate of the p₁ price offer curve against p₁ is the demand curve for good 1.

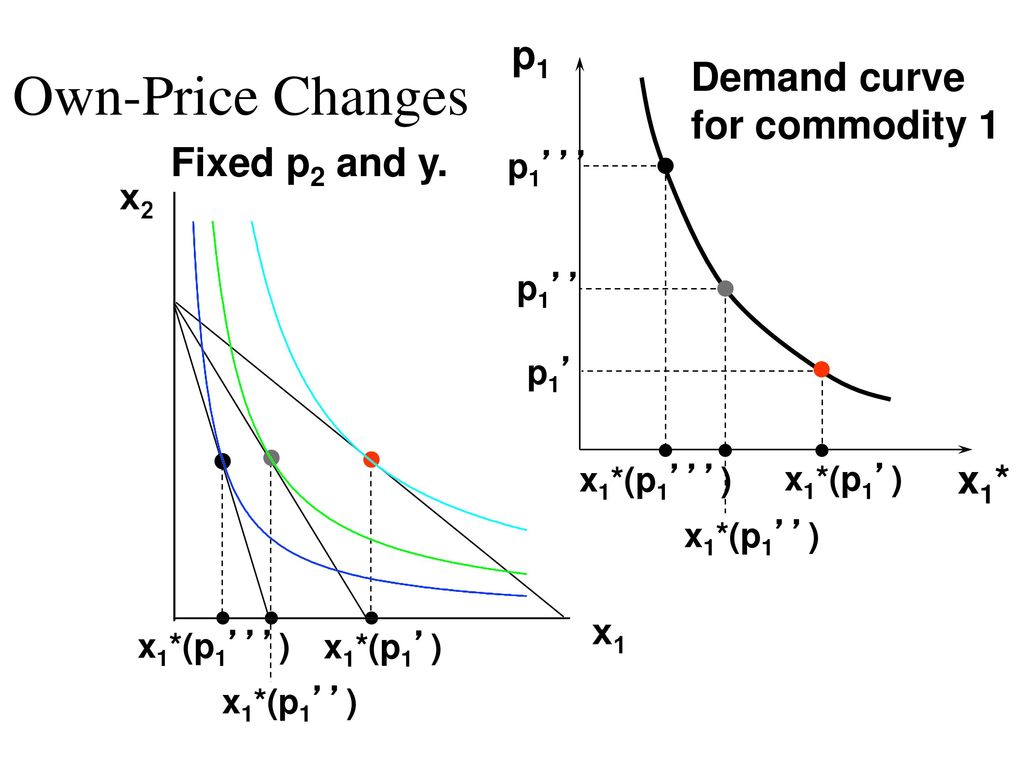
As the graph shows, the more that p₁ increases, the optimal amounts of good 1 and good 2 decrease. This is because the budget set becomes increasingly smaller.

Perfect Complements

The p₁ price offer curve for a perfect utility function would be a straight line in the form of x₂ = ax₁, as the bundles on that line will always be chosen as optimal bundles. The demand curve would have an x-intercept at y/p₂ and no vertical intercept.

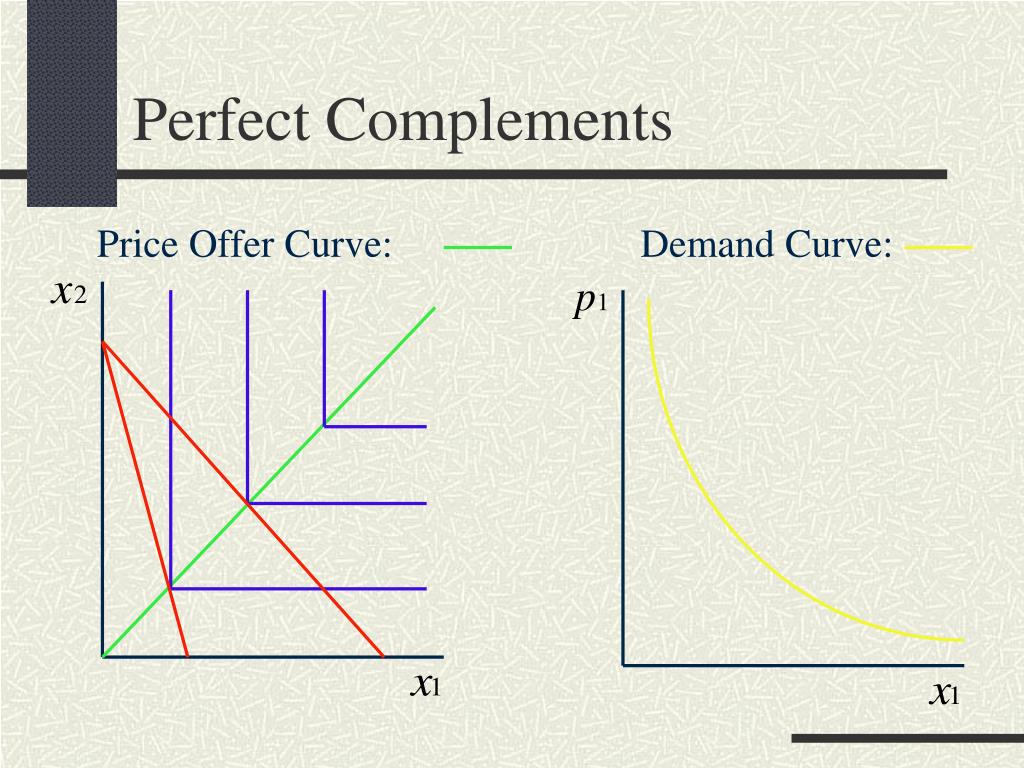
$$\text{Assuming that a = 1, the optimal amounts of goods 1 and 2 are: } \\ x_1^* (p_1, p_2, y) = x_2^* (p_1, p_2, y) = \frac{y}{p_1 + p_2} \\ \text{As } x_1 \rightarrow 0, x_1^* = x_2^* \rightarrow \frac{y}{p_2} \\ \text{As } x_1 \rightarrow \infty, x_1^* = x_2^* \rightarrow 0 \\$$

Perfect Substitutes

The optimal amounts of the goods are given by the following:

$$x_1^* (p_1, p_2, y) = \left\{ \begin{array}{lr} 0, & \text{if } p_1 > p_2\\ y / p_1, & \text{if } p_1 < p_2 \end{array} \right\} \\ x_2^* (p_1, p_2, y) = \left\{ \begin{array}{lr} 0, & \text{if } p_1 < p_2\\ y / p_2, & \text{if } p_1 > p_2 \end{array} \right\} \\$$

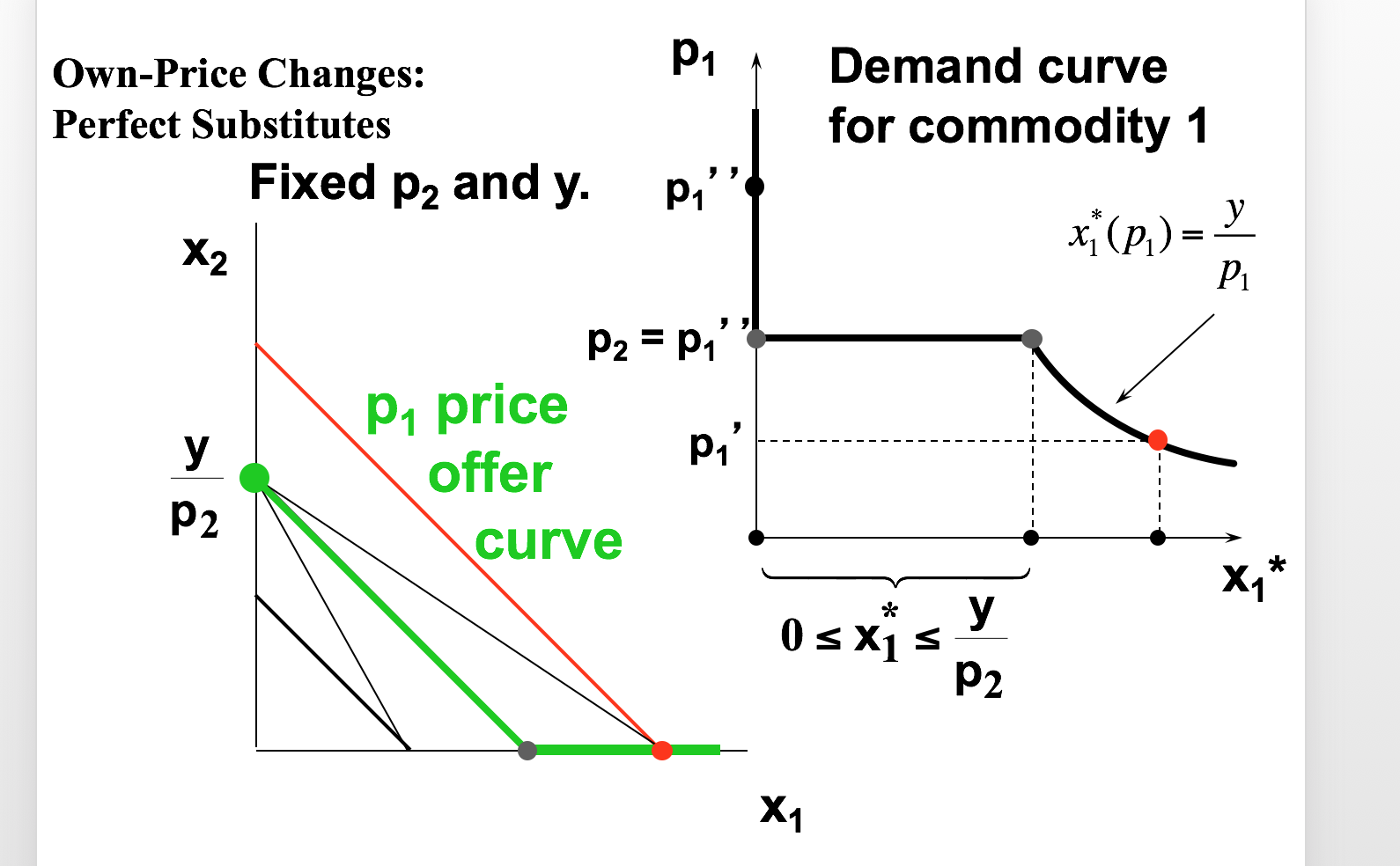
• The price offer curve has three pieces; when p1 > p2, p1 == p2, and p1 < p2
  • Note how the p1 < p2 case resembles the Cobb-Douglas indifference curve; this is because you are buying x1 such that x1p1 = y, which is the same as the Cobb-Douglas curves