Well-Behaved Preferences and Intro to Utility

Preferences Chapter

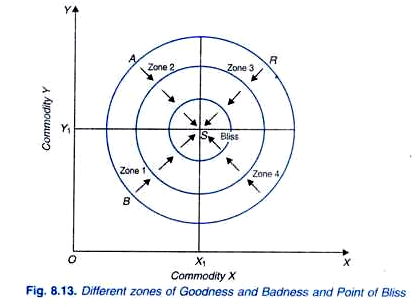
Preferences Exhibiting Satiation

• A bundle that is strictly preferred to any other bundle is a satiation point or bliss point
  • The existence of a satiation point implies that an excess of one or more commodities turns it into a bad but being below said point makes those commodities goods
  • Getting closer to the satiation point means that the rank order increases, so the indifference curves about a satiation point are circles

Well-Behaved Preferences

• A preference relation is well-behaved if it is both monotonic and convex
  • Monotonicity: More of any commodity is always preferred, implying that there is no satiation point and that every commodity is a good
  • Convexity: Mixtures of bundles are at least weakly preferred to the component bundles themselves
    • You can create a mixture of two bundles by using parts of two bundles
    • For example, a mixture bundle z can be created using two component bundles x and y via z = 0.5x + 0.5y
    • Essentially, this means that if you draw a line between any two points, then any point on said line would be strictly preferred to the endpoints of that line, meaning that the indifference curves must be convex, or concave up

$$\text{Let the mixture bundle } z = (t x_1 + (1 - t) y_1 , t x_2 + (1 - t) y_2) \\ \text{If the preference relations are strictly convex, then } z \succ x \text{ and } z \succ y \text{ for } 0 < t < 1 \\ \text{If the preference relations are weakly convex, then at least } \\ \text{one mixture bundle z in } 0 < t < 1 \text{ is equally preferred to a component bundle}$$

• In this graph, plotting a line between any two points will provide a set of bundles that are strongly preferred to the end points

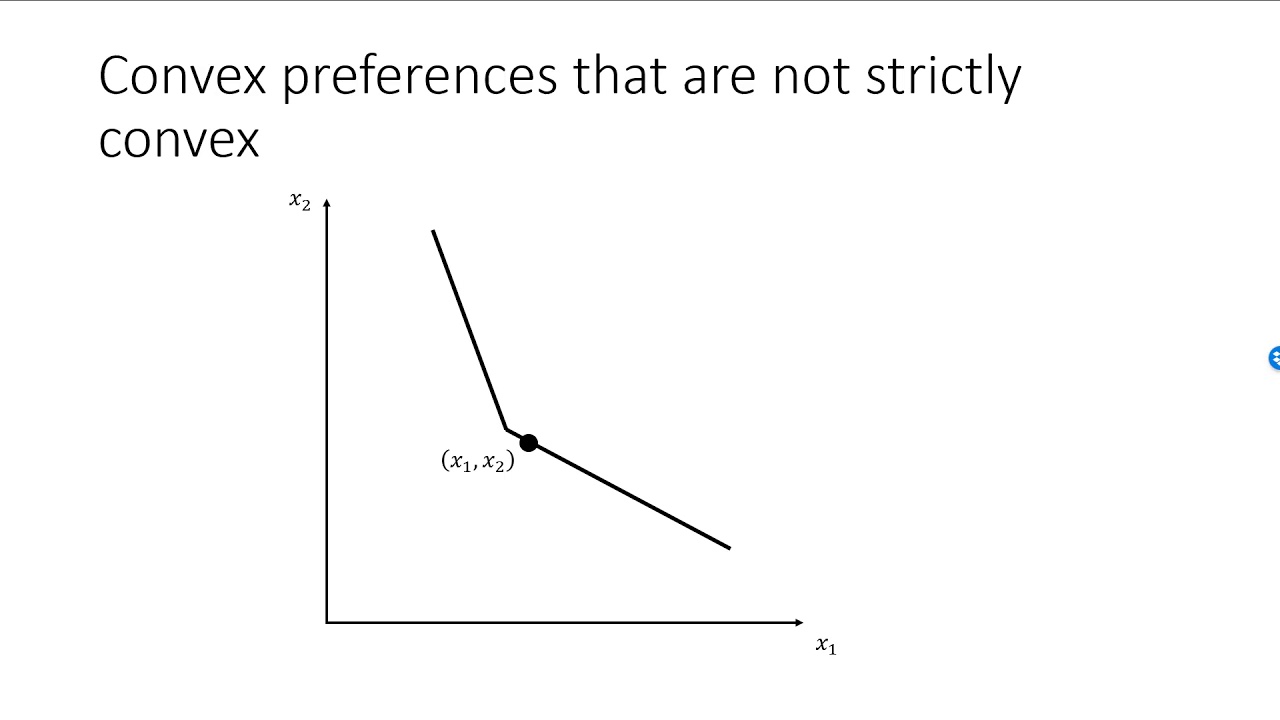
• In this graph, some of the lines between two points will have points that are equally preferred to the endpoints

• This graph is not convex if both of the commodities are goods, as any lines drawn between two points will not be preferred
• If both of the commodities are bads, then this graph is convex

Slopes of ICs

• The slope of an indifference curve is known as its marginal rate of substitution (MRS)
  • In other words, the MRS at a certain point is the slope of the IC at said point

$$\text{Considering the point x', } MRS(x') = \frac{d x_1}{d x_2} \text{ at x'.}$$

• At x’, the MRS is the rate at which the consumer is willing to exchange commodity 2 for a small amount of commodity 1
  • If both commodities are goods or bads, then the MRS will always be negative, as the ICs are negatively sloped
  • If one commodity is a good and the other a bad, then the MRS will always be positive, as the ICs are positively sloped
• If preferences are strictly convex, then the MRS will always increase with x₁; this is known as diminshing MRS, as the MRS is decreasing in absolute value
• If preferences are non-convex, then the MRS will actually decrease with x₁, and if they are weakly convex, then the MRS will be equal to 0 at some points

Utility Chapter

Utility Functions

• A preference relation that is complete, reflexive, transitive, and continuous can be represented by a continuous utility function
  • Continuity implies that small changes to a consumption bundle causes small changes to the preference level; there are no “jumps” like a step function
• A utility function U(x) represents a preference relation, ≽, if and only if

$$\text{A utility function U(x) repreresents a preference relation ≽ if and only if } \\ x' \succsim x'' \iff u(x') \geq u(x'') \\ x' \succ x'' \iff u(x') > u(x'') \\ x' \sim x'' \iff u(x') = u(x'') \\$$

• With preference relations, we cannot determine the magnitude of preference (i.e. x₁ is 3x preferred to x₂); the same applies to utility functions
  • e.g. u(x) = 6, u(y) = 2 only implies that x is preferred to y, but not that x is 3x preferred to y
• All bundles on the same indifference curve will all have the same utility level